[서울기온예측][pytorch][DNN 2] DNN으로 y=sin(x) 예측해보기, DNN 코드 이해하기
- 개요
하루 뒤 서울 평균기온을 예측하는 것이 목표지만 그 전에 간단하게 sin(x)를 예측하는 DNN을 만들어보겠습니다.
pytorch, tensorflow와 같은 라이브러리를 쓰면 DNN 모델을 만드는 것은 쉽고, 그마저도 ChatGPT나 Grok3처럼 언어모델에게 DNN 모델을 만들어달라고 요청하면 되는 세상입니다.
그러니 DNN 모델을 사용만 하는 입장에서는 DNN 모델의 코드를 이해하는 것이 중요합니다.
이번 포스트의 목표는 DNN 모델 모델 학습시 알아야하는 개념을 이해하고, 코드의 흐름 및 과정을 살펴보는 것입니다.
배경지식이 거의 필요없는 친숙한 함수인 y=sin(x)를 예측하면서 개념과 코드의 과정을 이해해보겠습니다.
- 학습(train), 검증(valid), 테스트(test)기간으로 분리하는 이유
선형회귀 모델에서는 자료를 학습, 테스트기간으로 분리했지만 DNN에서는 학습, 검증, 테스트기간으로 분류합니다.
선형회귀 모델은 학습기간 자료를 이용해서 평균 제곱 오차를 최소화시키는 선형회귀식을 구합니다.
이 식은 단 하나이며 테스트기간에 대한 예측을 수행하고, 이 결과로 모델의 성능을 검증합니다.

하지만 DNN 모델을 만들 때는 검증기간이라는 게 필요합니다.
검증기간이 필요한 근본적인 이유는 DNN 모델은 학습을 할수록 학습기간에 대한 성능이 거의 항상 좋아지기 때문입니다(학습할 때마다 오차가 계속 줄어들어 최적의 시점을 찾지 못함).
DNN 모델을 학습할 때는 아래의 과정을 반복합니다.
학습을 반복하면 다음 세대(epoch) DNN 모델의 오차가 감소하므로 언제까지 학습을 해야하는지 정할 기준이 필요합니다.
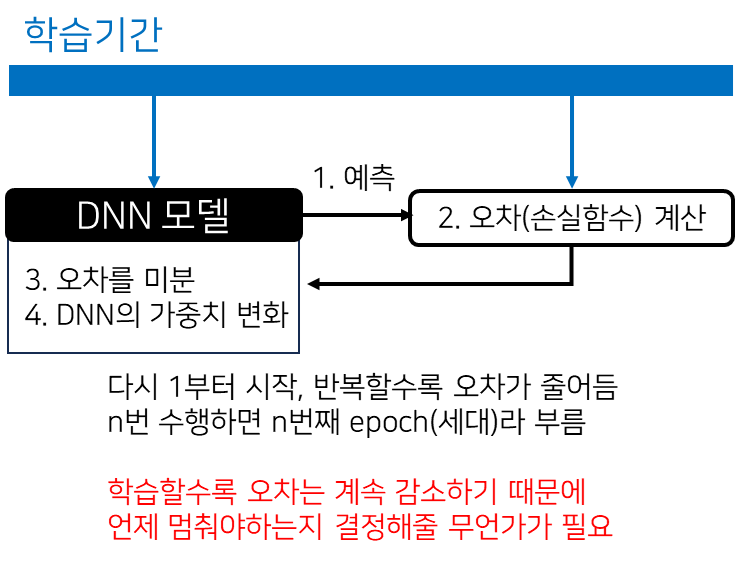
학습을 언제 중단할지, 몇 번째 세대의 DNN 모델을 쓸 지 결정하기 위해 검증기간이 필요합니다.
DNN 모델로 학습기간의 오차만이 아니라 검증기간의 오차를 구할 수 있습니다.
일반적으로 DNN 모델을 계속 학습시킬 경우 처음에는 학습기간 오차, 검증기간 오차가 모두 줄어들지만 어느 시점부터 검증기간 오차가 증가합니다.
이는 DNN 모델이 너무 학습기간만 맞출 수 있게 학습된 상태로 모델이 학습기간에 과적합(overfitting)된 것입니다.
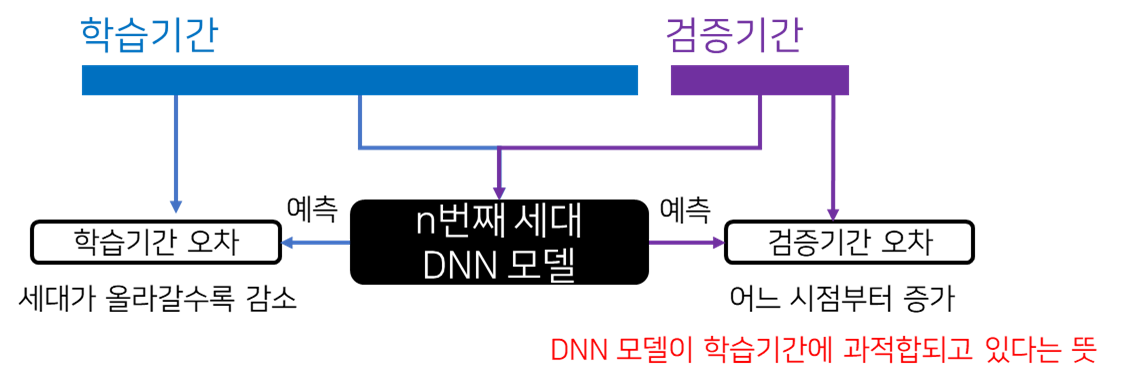
검증기간 오차로 몇 번째 세대의 모델을 쓸지 결정하고(검증기간 오차가 정확히 어떤 조건을 충족할 때의 세대를 쓸지 정하는 것은 만드는 사람 마음) 그 다음 테스트기간으로 성능 평가를 합니다.
이러한 이유로 자료를 학습기간, 검증기간, 테스트기간의 세 기간으로 나누어야 합니다.
- sin(x)를 예측하는 DNN 모델
1. 데이터 전처리
딥러닝 모델을 만들 때 쓰는 라이브러리는 pytorch, tensorflow가 있는데 전 pytorch 라이브러리를 사용합니다.
import numpy as np
import torch
# y = sin(x) 자료 만들, x는 입력, y는 출력(예측하는 값)
PI = np.pi
x_full = np.linspace(-10*PI, 10*PI, 1000)
y_full = np.sin(x_full)
"""
자료를 학습(train), 검증(valid), 테스트(test)로 나누어야 합니다.
보통 8:1:1로 나누므로
학습기간은 -10 ~ 6 (16)
검증기간은 6~8 (2)
테스트기간은 8~10 (2)
"""
train_idx = x_full <= 6 * PI
valid_idx = (x_full > 6*PI) & (x_full <= 8*PI)
test_idx = x_full > 8*PI
"""
pytorch 모델의 입력 자료는 tensor 타입으로 전달해야합니다.
torch.FloatTensor로 자료형을 변환합니다.
그리고 reshape(-1, 1)을 써서 [n, 1]의 차원으로 만듭니다.
"""
x_train = torch.FloatTensor(x_input[train_idx]).reshape(-1, 1)
y_train = torch.FloatTensor(y_full[train_idx]).reshape(-1, 1)
x_valid = torch.FloatTensor(x_input[valid_idx]).reshape(-1, 1)
y_valid = torch.FloatTensor(y_full[valid_idx]).reshape(-1, 1)
x_test = torch.FloatTensor(x_input[test_idx]).reshape(-1, 1)
y_test = torch.FloatTensor(y_full[test_idx]).reshape(-1, 1)
2. DNN 모델 구축
pytorch 라이브러리로 DNN 모델을 짜면 아래와 같습니다.
저번 포스트에서 활성화함수로 ReLU()를 언급했는데 Tanh()를 쓴 이유는 활성화함수로 Tanh()를 쓰니까 예측 성능이 좋기 때문입니다. ReLU() 함수는 x < 0 구간에서 값이 모두 0이므로 sin(x)를 학습하기에는 좀 부적절한가 봅니다.
import torch.nn as nn
class DNN(nn.Module):
def __init__(self):
super(DNN, self).__init__() # pytorch에 정의된 nn.Module 클래스를 상속시켜서 만듭니다
self.network = nn.Sequential(
nn.Linear(1, 8), # 입력 자료로 x_full을 넣을거고 [n x 1]차원이므로 입력 변수는 1개
nn.Tanh(),
nn.Linear(8, 32),
nn.Tanh(),
nn.Linear(32, 8),
nn.Tanh(),
nn.Linear(8, 1), # sin(x)값 하나를 예측하므로 출력도 1개
)
def forward(self, x):
return self.network(x)

3. DNN 모델 학습
모델 선언: model 변수
사용할 오차 선언: optimizer 변수
오차를 미분해서 감소시키는 과정에서 필요, 속도를 설정: optimizer 변수
학습 속도 변화 조건 설정: scheduler 변수
train_model이라는 함수를 만들어서 학습합니다.
train_model 함수는 학습기간, 검증기간의 x(입력자료), y(예측할 변수) 받는데요.
학습과정에서 하나 짚고 넘어갈 것이 있습니다.
우린 총 1000개의 자료를 만들었고 8:1:1 비율로 분리했으므로 학습기간의 자료 수는 800개입니다.
이 코드에서 주의할 점이 하나 있습니다.
여기서는 학습시 1번의 epoch마다 학습기간 800개 값을 모델에 넣은 다음 오차를 계산하고 가중치를 업데이트합니다.
보통은 학습기간의 전체 자료로 오차를 구하는 것이 아니라 batch_size를 정해서 이 크기대로 학습기간의 자료를 짤라서 하나씩 넣는 식으로 학습합니다.
예를 들어 batch_size=32라면 800개의 자료를 32개 단위로 나눈 다음(이걸 batch라 부름) 각 batch마다 오차를 구하고 가중치를 업데이트합니다.
나머지는 자세히 설명하기에는 분량이 너무 많아 코드에 간단하게 설명을 작성합니다.
model = DNN() # 모델 선언
criterion = nn.MSELoss() # MSE 오차 사용
optimizer = torch.optim.Adam(model.parameters(), lr=0.001) # lr로 학습 속도 결정
scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer, 'min', patience=50, factor=0.5) # 50세대 동안 개선 없으면 학습률을 0.5배, 반으로 줄임
def train_model(model, x_train, y_train, x_valid, y_valid, epochs=5000):
train_losses = []
valid_losses = []
best_valid_loss = float('inf')
best_model_path = 'best_model.pth' # 검증기간 오차가 제일 작은 모델 저장
for epoch in range(epochs):
model.train() # 학습모드
optimizer.zero_grad() # 오차의 기울기(미분)값을 학습에 사용하는데 0으로 설정해서 이전값 제거
outputs = model(x_train)
loss = criterion(outputs, y_train) # 오차 계산
loss.backward() # 오차의 기울기값 계산
optimizer.step() # 오차의 기울기값을 모델의 가중치에 반영
model.eval()
with torch.no_grad():
valid_outputs = model(x_valid)
valid_loss = criterion(valid_outputs, y_valid)
train_losses.append(loss.item()) # 세대별 학습기간 오차 저장
valid_losses.append(valid_loss.item()) # 세대별 검증기간 오차 저장
scheduler.step(valid_loss)
if valid_loss.item() < best_valid_loss: # 검증오차가 제일 작은 모델을 저장
best_valid_loss = valid_loss.item()
torch.save(model.state_dict(), best_model_path)
print(f'Epoch {epoch}: New best model saved with valid_loss: {best_valid_loss:.4f}')
if epoch % 100 == 0:
print(f'Epoch {epoch}, Train Loss: {loss.item():.4f}, Valid Loss: {valid_loss.item():.4f}, LR: {optimizer.param_groups[0]["lr"]:.6f}')
return train_losses, valid_losses, best_model_path
train_losses, valid_losses, best_model_path = train_model(model, x_train, y_train, x_valid, y_valid)
4. 결과 시각화
학습자료, 검증자료로 최적의 모델 저장했으니 테스트기간의 자료로 예측 성능을 확인합시다.
import matplotlib.pyplot as plt
best_model = DNN()
best_model.load_state_dict(torch.load(best_model_path))
best_model.eval()
with torch.no_grad():
y_pred = best_model(x_test)
# 7. 결과 시각화
plt.figure(figsize=(15, 5))
plt.plot(x_full, y_full, 'b-', label='True sin(x)')
plt.plot(x_full[test_idx], y_pred.numpy(), 'r--', label='Predicted sin(x) (Best Model)')
plt.axvline(x=6*PI, color='g', linestyle='--', label='Train/Valid split')
plt.axvline(x=8*PI, color='y', linestyle='--', label='Valid/Test split')
plt.xlabel('x')
plt.ylabel('sin(x)')
plt.legend()
plt.title('Sin(x) Prediction using [x, x % (2π)] as Input')
plt.show()
# 학습 곡선 플롯
plt.figure(figsize=(10, 5))
plt.plot(train_losses, label='Train Loss')
plt.plot(valid_losses, label='Valid Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend()
plt.title('Training and Validation Loss')
plt.show()
# 테스트 성능 평가
with torch.no_grad():
test_outputs = best_model(x_test)
test_loss = criterion(test_outputs, y_test)
print(f'Test Loss of Best Model: {test_loss.item():.4f}')
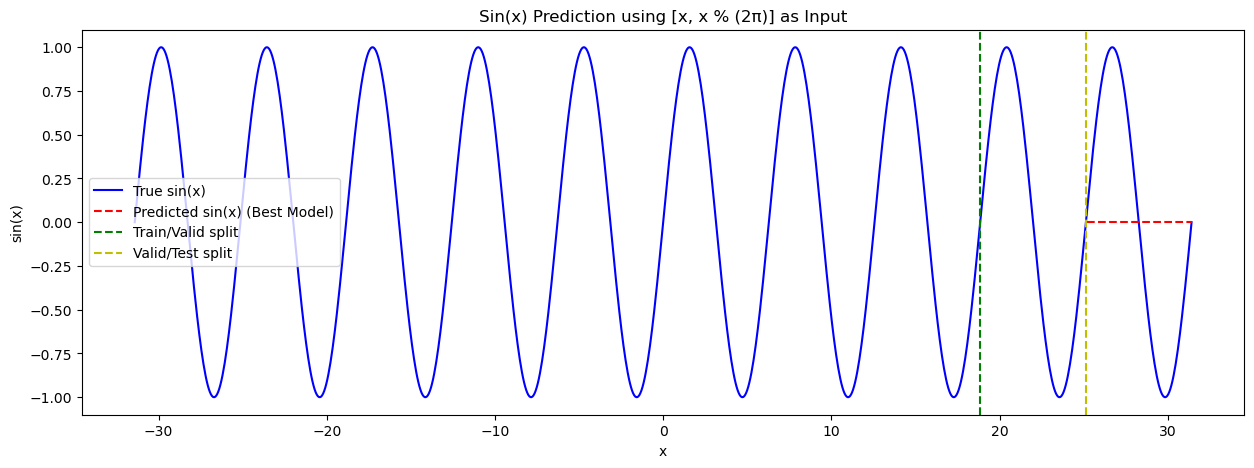
빨간선이 테스트기간을 예측한 것인데 전혀 맞지 않네요...
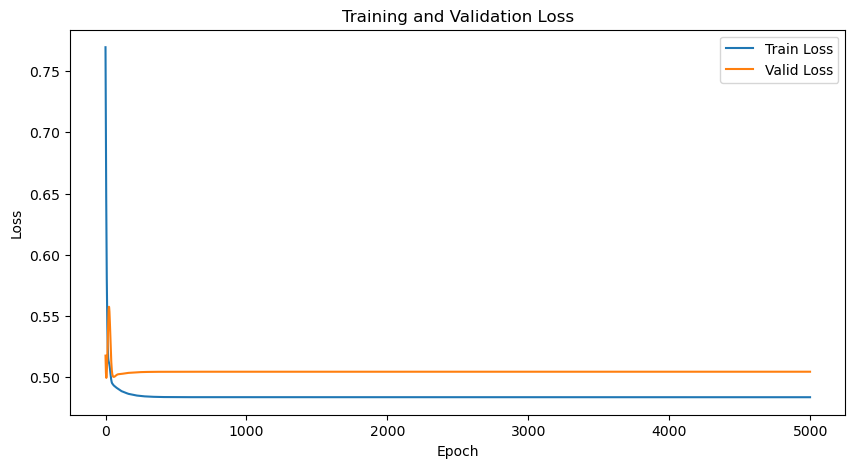
세대(epoch)별 학습오차(파란선)와 검증오차(주황선)입니다.
세대가 지날수록 학습오차는 계속 감소하고 검증오차는 100 세대 이전에 최솟값이 있는듯합니다.
- sin(x)를 맞출 수 있게 DNN 모델을 개선
sin(x)는 2*PI 주기로 도는 함수니까 입력자료로 x만 쓰지 않고 x를 2*PI 나눈 몫과 나머지, 2개의 입력자료를 쓰겠습니다.
입력자료의 차원이 바뀌니 DNN 모델의 시작 차원을 2로 만들어줘야합니다.
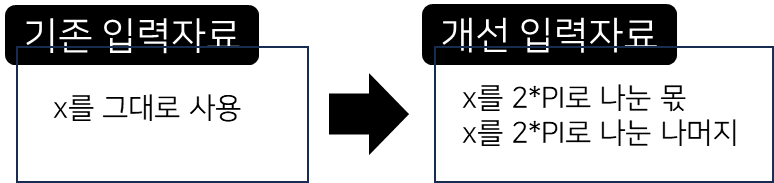
수정한 전체 코드를 적겠습니다.
import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
PI = np.pi
x_full = np.linspace(-10*PI, 10*PI, 1000)
y_full = np.sin(x_full)
x_full_int = x_full // (2*PI) # 몫
x_full_mod = x_full % (2*PI) # 나머지
# x_input에 x_full_int, x_full_mod를 합쳐서 DNN에 넣어야함
x_input = np.stack([x_full_int, x_full_mod], axis=1) # shape: (1000, 2)
train_idx = x_full <= 6*PI
valid_idx = (x_full > 6*PI) & (x_full <= 8*PI)
test_idx = x_full > 8*PI
x_train = torch.FloatTensor(x_input[train_idx]) # shape: (train_size, 2)
y_train = torch.FloatTensor(y_full[train_idx]).reshape(-1, 1)
x_valid = torch.FloatTensor(x_input[valid_idx]) # shape: (valid_size, 2)
y_valid = torch.FloatTensor(y_full[valid_idx]).reshape(-1, 1)
x_test = torch.FloatTensor(x_input[test_idx]) # shape: (test_size, 2)
y_test = torch.FloatTensor(y_full[test_idx]).reshape(-1, 1)
import torch.nn as nn
class DNN(nn.Module):
def __init__(self):
super(DNN, self).__init__()
self.network = nn.Sequential(
nn.Linear(2, 8), # 입력차원이 2차원이므로 2로 바꿔야함
nn.Tanh(),
nn.Linear(8, 32),
nn.Tanh(),
nn.Linear(32, 8),
nn.Tanh(),
nn.Linear(8, 1),
)
def forward(self, x):
return self.network(x)
model = DNN()
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer, 'min', patience=50, factor=0.5)
def train_model(model, x_train, y_train, x_valid, y_valid, epochs=5000):
train_losses = []
valid_losses = []
best_valid_loss = float('inf')
best_model_path = 'best_model.pth'
for epoch in range(epochs):
model.train()
optimizer.zero_grad()
outputs = model(x_train)
loss = criterion(outputs, y_train)
loss.backward()
optimizer.step()
model.eval()
with torch.no_grad():
valid_outputs = model(x_valid)
valid_loss = criterion(valid_outputs, y_valid)
train_losses.append(loss.item())
valid_losses.append(valid_loss.item())
scheduler.step(valid_loss)
if valid_loss.item() < best_valid_loss:
best_valid_loss = valid_loss.item()
torch.save(model.state_dict(), best_model_path)
print(f'Epoch {epoch}: New best model saved with valid_loss: {best_valid_loss:.4f}')
if epoch % 100 == 0:
print(f'Epoch {epoch}, Train Loss: {loss.item():.4f}, Valid Loss: {valid_loss.item():.4f}, LR: {optimizer.param_groups[0]["lr"]:.6f}')
return train_losses, valid_losses, best_model_path
train_losses, valid_losses, best_model_path = train_model(model, x_train, y_train, x_valid, y_valid)
import matplotlib.pyplot as plt
best_model = DNN()
best_model.load_state_dict(torch.load(best_model_path))
best_model.eval()
with torch.no_grad():
y_pred = best_model(x_test)
# 7. 결과 시각화
plt.figure(figsize=(15, 5))
plt.plot(x_full, y_full, 'b-', label='True sin(x)')
plt.plot(x_full[test_idx], y_pred.numpy(), 'r--', label='Predicted sin(x) (Best Model)')
plt.axvline(x=6*PI, color='g', linestyle='--', label='Train/Valid split')
plt.axvline(x=8*PI, color='y', linestyle='--', label='Valid/Test split')
plt.xlabel('x')
plt.ylabel('sin(x)')
plt.legend()
plt.title('Sin(x) Prediction using [x, x % (2π)] as Input')
plt.show()
# 학습 곡선 플롯
plt.figure(figsize=(10, 5))
plt.plot(train_losses, label='Train Loss')
plt.plot(valid_losses, label='Valid Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend()
plt.title('Training and Validation Loss')
plt.show()
# 테스트 성능 평가
with torch.no_grad():
test_outputs = best_model(x_test)
test_loss = criterion(test_outputs, y_test)
print(f'Test Loss of Best Model: {test_loss.item():.4f}')
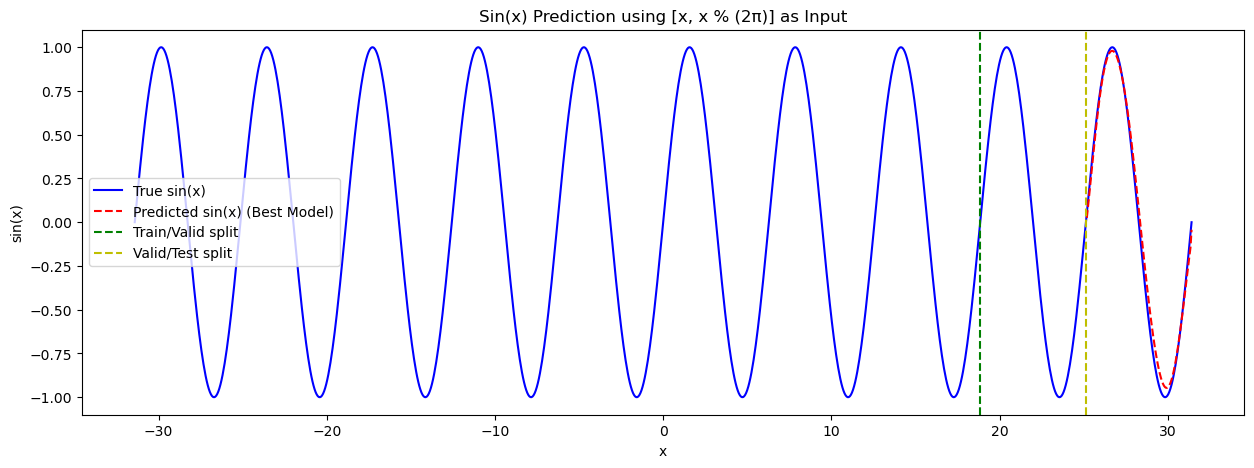
예측한 결과를 봅시다.
빨간선이 이제 파란선(sin(x))과 꽤 잘 맞습니다.
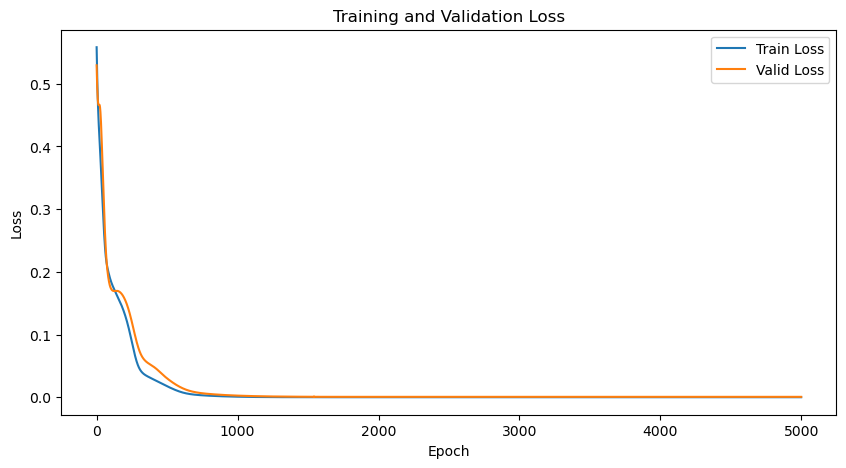
학습 오차와 검증 오차는 0까지 계속 감소합니다.
- 결과 및 다음 방향
x를 그냥 넣는 것이랑 x를 2*PI로 나눈 몫, 나머지를 넣는 것의 예측 결과는 다르다.
입력 변수에 특정한 작업을 하면 예측 성능을 향상시킬 수 있다.
DNN으로 하루 뒤 서울 일평균기온을 예측해보자.